Multi-partite entanglement
Entanglement is one of the most fundamental concepts in quantum information science, and is the cornerstone in many applications in quantum computing, communication and cryptography. Roughly speaking, two or more quantum systems are said to be entangled if their states cannot be separately described any more, but only as a whole. Originally only bi-partite entanglement was considered, but the last two decades has seen an increasing interest in multi-partite entanglement, that considers more than two quantum systems.
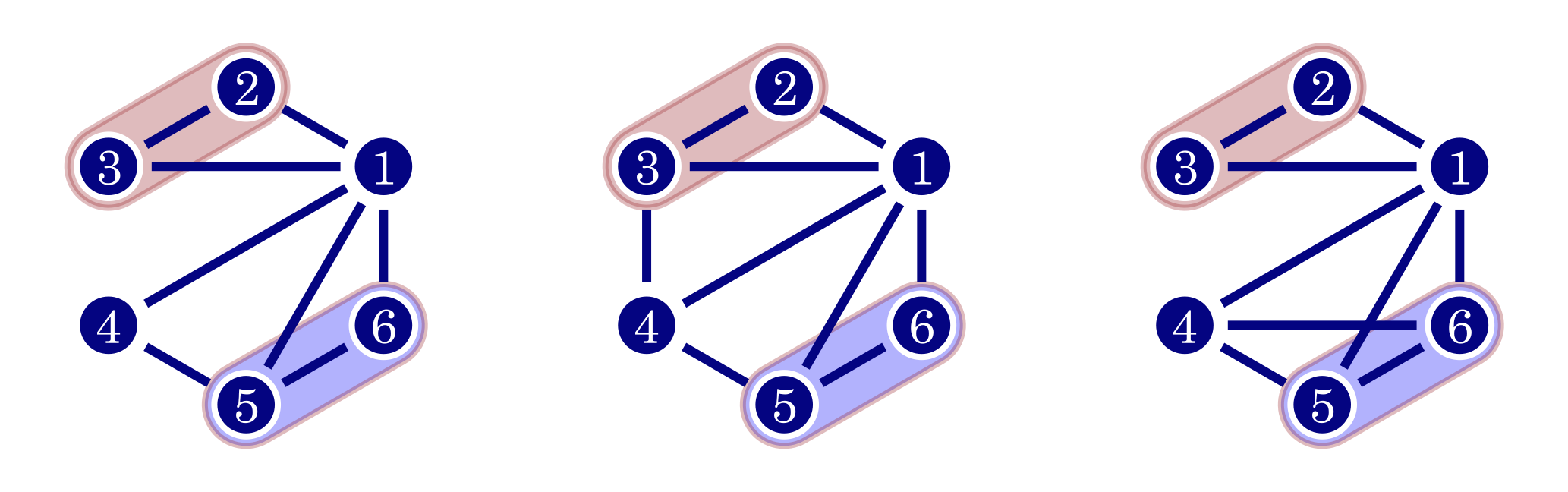
An indispensable tool in the study of multi-partite entanglement is the graph state, a particular type of multi-partite entangled state that conveys many of their interesting properties, while also having a clear graphical representation. My research in multi-partite entanglement has particularly focussed on the equivalence of different forms of multi-partite entanglement in quantum networks. Of particular interest was:
- Characterising different types of entanglement
- Questions like ‘can I obtain quantum state B from quantum state A within a quantum network, without having to create new entanglement in between?’
Overview of publications
An overview of my publications in the topic is as follows:
1. Extracting GHZ states from linear cluster states (arxiv, Published)
de Jong, Hahn, Tcholtchev, Hauswirth, Pappa - Phys. Rev. Research 6, 013330 (2023).
- A complete characterization of how GHZ states can be realized from linear cluster states in quantum networks.
2. Distinguishing graph states by the properties of their marginals (arxiv, Published)
Vandré*, de Jong*, Hahn, Burchardt, Gühne, Pappa - Phys. Rev. A 111, 052449 (2025). * these authors have contributed equally.
- A study on how to detect distinguish different forms of entanglement in quantum networks by using the properties of reduced states.